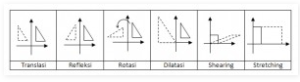
TRANSFORMASI GEOMETRI

Transformasi merupakan suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. Jenis-jenis dari transformasi yang dapat dilakukan antara lain :

Translasi (Pergeseran)
Refleksi(Pencerminan)
Rotasi(Perputaran)
Dilatasi(Penskalaan)

Berikut ini ilustrasinya :

TRANSLASI / PERGESERAN

Berdasarkan gambar di atas, segitiga ABC yang mempunyai koordinat A(3, 9), B(3, 3), C(6, 3) ditranslasikan:

Berdasarkan penjelasan diatas, maka untuk mencari nilai translasi dapat digunakan rumus sebagai berikut :

dimana :

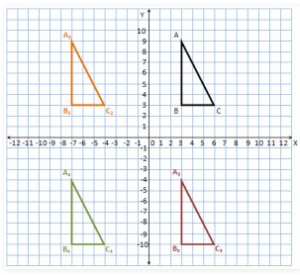
a menyatakan pergeseran horizontal (kekanan+, kekiri-)
b menyatakan pergeseran vertikal (keatas+,kebawah-)

Contoh Soal :

Soal No. 1
a) Tentukan bayangan dari titik A (2, 3) oleh translasi T = (7, 8)

b) Tentukan bayangan dari

titik A (5, 10) oleh translasi

c) Tentukan bayangan dari titik A (1, 2) oleh translasi T = (1, 2) dilanjutkan oleh translasi U = (3, 4)

Pembahasan
Bayangan dari titik A oleh suatu transformasi namakan A’ Dua model yang biasa dipakai sebagai berikut:

Hasilnya akan sama saja, hanya sedikit beda cara penulisan, sehingga:

a) Bayangan dari titik A (2, 3) oleh translasi T = (7, 8)

b) Bayangan dari titik A (5, 10) oleh translasi

c) Bayangan dari titik A (1, 2) oleh translasi T = (1, 2) dilanjutkan oleh translasi U = (3, 4)

Soal No. 2
Disediakan suatu persamaan garis lurus
Y = 3x + 5
Tentukan persamaan garis lurus yang dihasilkan oleh translasi T = (2, 1)

Pembahasan
Ada beberapa cara diantaranya:
Cara pertama:
Posisi titik (x, y) oleh translasi T = (2, 1) adalah:
x’ = x + 2 → x = x’ – 2
y’ = y + 1 → y = y’ – 1

Masukkan nilai x dan y yang baru ke persamaan asal
y = 3x + 5
(y’ – 1 ) = 3(x’ – 2) + 5

Tinggal selesaikan, ubah lambang y’ dan x’ ke y dan x lagi:
y – 1 = 3x – 6 + 5
y = 3x – 6 + 5 + 1
y = 3x

Cara kedua:
Ambil dua buah titik dari persamaan y = 3x + 5
Misal:
Titik A, untuk x = 0 → y = 5 dapat titik A (0, 5)
Titik B, untuk Y = 0 → x = –⁵ /₃ dapat titik B (– ⁵/₃ , 0)

Translasikan Titik A dan B dengan T = (2,1)
A’ (0 + 2, 5 +1) = A’ (2, 6)
B’ (-5/3 + 2, 0 + 1) = A’ (1/3, 1)

Buat persamaan garis yang melalui kedua titik itu:

Cara ketiga
Dengan rumus yang sudah jadi atau rumus cepat:

ax + by = c
Translasi T (p, q)
Hasil :
ax + by = c + ap + bq

Rumus ini untuk bentuk seperti soal di atas, jangan terapkan pada bentuk-bentuk yang lain, nanti salah.
y = 3x + 5
atau
3x − y = − 5
oleh T = (2,1)

Hasil translasinya adalah:
3x − y = − 5 + (3)(2) + (− 1)(1)
3x − y = − 5 + 6 − 1
3x − y = 0
atau
y = 3x

TRANSFORMASI GEOMETRI

Tinggalkan Balasan Batalkan balasan